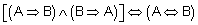Konzepte für Lehrende
Der kognitiv-rationale Präferenztyp erwartet von den Lehrenden vor allem Fachkompetenz. Er ist ein an der kausalen Logik orientierter Lerner.
Alle Dinge, die er lernt, müssen in sein rationales Schema passen. Lernende dieses Präferenztyps erwarten, dass der Lernprozess vor allem »logisch«
vermittelt wird. Aus diesem Grunde ist es für Lehrende wichtig, sich mit den Grundlagen der Logik auseinander zu setzen.
Der Lehrende sollte wissen, dass sich der Denker Zusammenhänge erschließt, indem er diese erklärbar (Erklärungswissen) macht.
Ein so strukturierter Mensch verfügt über eine hohe sprachliche Intelligenz, da die Sprache sein Zugangskanal
für alle Lerninhalte ist. Deshalb kann der Lehrende sehr gut mit den Texttechniken arbeiten, wobei es auf die Kenntnisse von Zusammenhängen (Überblick) ankommt.
Der Denker lässt sich aber auch über angemessene Methoden, wie z.B. die sokratische Methode motivieren. Wesentlich ist,
dass bei den Lernvorgängen der Zusammenhang über Formen des Erkennens (kognitiv) vermittelt wird.
Sokratische Methode
Die sokratische Methode, auch Mäeutik (griech. Hebammenkunst) genannt, gilt als Methode der Wahrheitsfindung. Diese Methode geht auf den griechischen
Philosoph Sokrates, den Sohn der Hebamme Phainarete, zurück.
Mit Hilfe geschickt gestellter Fragen bewirkte Sokrates bei seinen Gesprächspartnern Zweifel. Wenn man zwischen mindestens zwei Ansichten über einen
Sachverhalt unterscheiden kann, entsteht Zweifel über die Richtigkeit der jeweiligen Ansicht. Kognitiv-rationales Denken wird gefördert, wenn der
Lehrende im Kommunikationsprozess durch die Fragen zum Nachdenken über denkbare andere Ansichten anregt. Während es sich bei Sokrates um einen Dialog
zwischen zwei Personen, handelt, wird die Methode mittlerweile auch im Gespräch mit mehreren angewandt. Heute wird unter der ‚Sokratischen Methode’ die
Art der Fragestellung und Gesprächsführung verstanden, die nach dem eigentlich Gemeinten forscht.
Die Lernenden sollen beim sokratischen Gespräch zu eigenen Ansichten über die Fragestellung gelangen. Im Gespräch werden individuelle Gedanken überprüft
und gegebenenfalls modifiziert bzw. korrigiert. Das Selbstvertrauen wird gesteigert, da die Urteile durch eigenes Denken und Argumentieren zu Stande
kommen.
Drei Vorgehensweisen können bei der sokratischen Methode unterschieden werden:
- Die Methode der Definition - Eine vorläufige Ausgangsdefinition bildet den Ausgangspunkt zur Entwicklung korrekter Begriffsdefinitionen.
- Die Methode der Induktion - Ausgehend von Erfahrungen des Alltagslebens gelangt man zu allgemeinen Aussagen.
- Die Methode der Ironie - Die Gesprächspartner werden in Widersprüche verwickelt.

- DefinitionEine Definition gibt die wesentlichen Merkmale an, um die Bedeutung eines Begriffs einzugrenzen und so die Eigenschaften von Gegenständen zu kennzeichnen. Meist wird ein Bezug zur nächsten Gattung oder der Unterschied zu einer anderen Gattung formuliert.
-
Aus der Sicht einer kognitiv-rationalen Präferenz ist die Definition ein Denkverfahren, mit dessen Hilfe die Bedeutung eines Zeichens oder eines Begriffs gekennzeichnet wird. Bei Definitionen gilt es Fehler zu vermeiden. Als typische Fehler gelten:
- Inadäquatheit: Wenn der Begriffsumfang (Klasse aller Gegenstände, die durch einen Begriff ausgedrückt werden) der Begriffsbestimmung (Eigenschaften eines Begriffs) gleicht.
- Zirkularität: Wenn ein Ausdruck mit Hilfe desselben Ausdrucks definiert wird.
- Definition von Unbekanntem durch Unbekanntes.
- Widersprüchlichkeit: Wenn eine Aussage bestreitet, was die andere behauptet.
- Unklarheit: Mehrdeutigkeiten gilt es auszuschließen.

- InduktionEin Thema wird vom Konkreten ausgehend allmählich abstrahierend untersucht. Durch den Vergleich von Einzelfällen und das Erkennen von Zusammenhängen können allgemeine, übergreifende Aspekte abgeleitet und formuliert werden. Unterschieden wird zwischen aufzählender Induktion (auch: Induktion durch einfache Aufzählung) und ausscheidender Induktion.
-
Bei der aufzählenden Induktion werden möglichst viele Einzeltatsachen zusammengetragen, um einen allgemeinen Satz formulieren zu können, der sich aus den einzelnen Tatsachen folgern lässt.Beispiel: Wenn jemand bisher nur weiße Schwäne gesehen hat, kann er die Hypothese aufstellen: Alle Schwäne sind weiß. Diese aufzählende Induktion ist aber unvollständig, da der Nachweis nur eines schwarzen Schwans die Hypothese widerlegt.Bei der ausscheidenden Induktion werden die nicht in Frage kommenden Aspekte aus der Gesamtzahl von möglichen Hypothesen ausgeschaltet.John Stuart Mill (1806 – 1873) unterscheidet fünf Methoden zur Untersuchung kausaler Zusammenhänge:
- Methode der Ähnlichkeit (Methode der Übereinstimmung). Suche nach einem gemeinsamen Umstand bei unterschiedlichen Erscheinungen.
- Methode des Unterschieds (Methode des einzigen Unterschieds). Es handelt sich um einen Wahrscheinlichkeitsschluss, da alle Unterschiede außer einem ausgeschlossen werden müssen.
- vereinigte Methode von Ähnlichkeit und Unterschied. Wenn sich beide Reihen unterscheiden, ist die eine Erscheinung Ursache oder Folge der anderen Erscheinung.
- Methode der Reste. Wenn bei einer Erscheinung die bekannten Teile abgezogen werden, muss der Rest dieser Erscheinung die Folge der übrigen Ursachen sein.
- Methode der begleitenden Veränderung. Wenn eine Erscheinung sich parallel zu einer anderen Erscheinung auf bestimmte Weise ändert, handelt es sich entweder um eine Folge oder eine Ursache dieser Erscheinung (kausaler Zusammenhang).
Von einzelnen Fällen und den Resultaten wird die Regel abgeleitet.Beispiel:- Platon war ein Mensch. Aristoteles war ein Mensch. Epikur war ein Mensch. (Fall, bzw. Fälle.)
- Platon ist gestorben. Aristoteles ist gestorben. Epikur ist gestorben. [Und mir geht's auch nicht besonders] (Resultate)
- Alle Menschen sind sterblich. (Regel.)